Correction DNB Maths – Juin 2022 – Centre Etrangers
Easymaths.fr vous propose des corrections détaillées des Dnb maths.
Exercice 1 : (points) QCM
Les deux parties de cet exercice sont indépendantes.
Partie A :
Cette partie est un questionnaire à choix multiples (QCM). Pour chaque question, trois réponses sont proposées, une seule est exacte. Recopier le numéro de la question et indiquer, sans justifier dans cette partie seulement, la réponse choisie.
1- Dans toute cette partie, on considère la fonction définie par : $$f(x)=2x+3$$ La représentation graphique de cette fonction est :
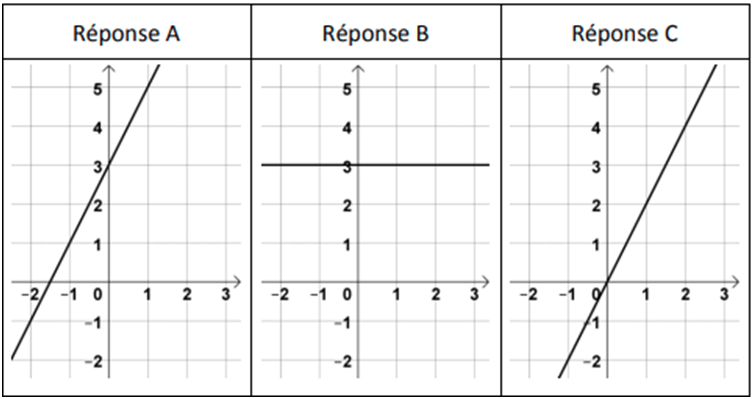
2- L’image de $-2$ par la fonction $f$ est…
Réponse A : $-7$
Réponse B : $-1$
Réponse A : $3$

3- Dans cette feuille de calcul extraite d’un tableur, la formule à saisir dans la cellule $\text{B2}$ avant de l’étirer vers la droite est :
Réponse A : $=\text{2*A1+3}$
Réponse B : $=\text{2*B1+3}$
Réponse A : $=\text{2*(-2)+3}$
Partie B :
1- Montrer que $(2c-1)(3x+4)-2x=6x^2+3x-4$
2- On considère le triangle $CDE$ tel que : $CD = 3,6$ cm ; $CE = 4,2$ cm et $DE = 5,5$ cm.
Le triangle $CDE$ est-il rectangle ?
Partie A
- Le coefficient directeur est $a=2>0$ : ce n’est donc pas la réponse B.
L’ordonnée à l’origine est $b=3\neq 0$ : ce n’est donc pas la réponse C.
Réponse A - L’image de $-2$ par la fonction $f$ est :
$\begin{align*} f(-2)&=2\times (-2)+3 \\
&=-4+3 \\
&=-1\end{align*}$
Réponse B - La formule à saisir est $=\text{2*B1+3}$.
Réponse B
Partie B
- Pour tout nombre $x$ on a
$\begin{align*} (2x-1)(3x+4)-2x&=6x^2+8x-3x-4-2x \\
&=6x^2+3x-4\end{align*}$
$\quad$ - Dans le triangle $CDE$ le plus grand côté est $[DE]$.
D’une part $DE^2=5,5^2=30,25$
D’autre part $CD^2+CE^2=3,6^2+4,2^2=30,6$
Par conséquent $DE^2\neq CD^2+CE^2$.
D’après la contraposée du théorème de Pythagore, le triangle $CDE$ n’est pas rectangle.
$\quad$
Exercice 2 : (points)
Le Paris-Nice est une course cycliste qui se déroule chaque année et qui mène les coureurs de la région parisienne à la région niçoise. L’édition 2021 s’est déroulée en $7$ étapes décrites ci-dessous :
$$\begin{array}{|c|c|c|l|c|}
\hline
\textbf{Étape}&\textbf{Date}&\textbf{Profil}&\phantom {1234123123}\textbf{Parcours}&\textbf{Distance}\\
\hline
1&\text{Dimanche 7 mars}&\text{Accidenté}&\text{Saint-Cyr-l’École} \to \text{Saint-Cyr-l’École}& 166 \text{km} \\
\hline
2&\text{Lundi 8 mars}&\text{Plat}&\text{Oinville-sur-Montcient} \to \text{Amilly}& 188 \text{km} \\
\hline
3&\text{Mercredi 10 mars}&\text{Accidenté}&\text{Chalon-sur-Saône} \to \text{Chiroubles}& 187,5 \text{km} \\
\hline
4&\text{Jeudi 11 mars}&\text{Plat}&\text{Vienne} \to \text{Bollène}& 200 \text{km} \\
\hline
5&\text{Vendredi 12 mars}&\text{Accidenté}&\text{Brignoles} \to \text{Biot}& 202,5 \text{km} \\
\hline
6&\text{Samedi 13 mars}&\text{Montagneux}&\text{Le Broc} \to \text{Valdeblore La Colmiane}& 119,5 \text{km} \\
\hline
7&\text{Dimanche 14 mars}&\text{Accidenté}&\text{Le Plan-du-Var} \to \text{Levens}& 93 \text{km} \\
\hline
\end{array}$$
- On étudie la série des distances parcourues par étape.
a. Calculer la distance moyenne parcourue par étape, arrondie au dixième de km.
b. Calculer la médiane des distances parcourues par étape.
c. Calculer l’étendue de la série formée par les distances parcourues par étape. - Un journaliste affirme : « Environ $57\%$ du nombre total d’étapes de cette édition se sont déroulées sur un parcours accidenté. » A-t-il raison ? Expliquer votre réponse.
- L’Allemand Maximilian SCHACHMANN a remporté la course en $28$ h $50$ min.
Le dernier au classement général a effectué l’ensemble du parcours en $30$ h $12$ min.
Combien de retard le dernier au classement a-t-il accumulé par rapport au vainqueur ? - L’Irlandais Sam BENNETT a remporté la première étape en $3$ h $51$ min. Déterminer sa vitesse moyenne en km/h, arrondie à l’unité, lors de cette étape.
- a. La distance moyenne parcourue est :
$\begin{align*} d_m&=\dfrac{166+188+187,5+200+202,5+119,5+93}{7} \\
&=\dfrac{1~156,5}{7} \\
&\approx 165,2\end{align*}$
La distance moyenne parcourue est environ égale à $165,2$ km.
b. On ordonne la série de valeurs dans l’ordre croissant :
$$93~;~119,5~;~166~;~187,5~;~188~;~200~;~202,5$$
$\dfrac{7}{2}=3,5$ : la médiane est donc la $4^{ème}$ valeur, c’est-à-dire $187,5$.
La médiane des distances parcourues par étapes est $187,5$ km.
c. $202,5-93=109,5$.
L’étendue de la série formée par les distances parcourues par étape est égale à $109,5$. - $4$ étapes sur les $7$ se sont déroulées sur un parcours accidenté.
$\dfrac{4}{7}\approx 0,57$.
Le journaliste a donc raison. - $30$ h $12$ min $- 28$ h $50$ min $= 1$ h $22$ min.
Le dernier au classement a donc accumulé $1$ h $22$ min de retard par rapport au vainqueur. - $51$ min $=0,85$ h
$\dfrac{166}{3,85}\approx 43$.
La vitesse moyenne du coureur est environ égale à $43$ km/h.
Exercice 3 : ( 21 points) Géométrie
On considère la figure suivante, où toutes les longueurs sont données en centimètre. Les points $C$, $A$ et $E$ sont alignés et les points $B$, $A$ et $D$ sont alignés. La figure n’est pas représentée en vraie grandeur.

- Prouver que le segment $[AB]$ mesure $4$ cm.
- En utilisant la question précédente, démontrer que les droites $(BC)$ et $(DE)$ sont parallèles.
- En déduire que la droite $(DB)$ est perpendiculaire à la droite $(DE)$.
- Calculer l’aire du triangle $ADE$ arrondie à l’unité.
- Dans le triangle $ABC$ rectangle en $B$ on a $\cos\widehat{BAC}=\dfrac{AB}{AC}$ soit $\cos(60)=\dfrac{AB}{8}$
Par conséquent $AB=8\cos(60)$ et donc $AB=4$ cm. - Dans les triangles $ABC$ et $ADE$ on a :
– $A$ appartient aux segments $[CE]$ et $[BD]$
– $\dfrac{AE}{AC}=\dfrac{19,2}{8}=2,4$ et $\dfrac{AD}{AB}=\dfrac{9,6}{4}=2,4$
Par conséquent $\dfrac{AE}{AC}=\dfrac{AD}{AB}$
D’après la réciproque du théorème de Pythagore les droites $(BC)$ et $(DE)$ sont parallèles. - La droite $(DE)$ est parallèle à la droite $(BC)$ et les droites $(DB)$ et $(BC)$ sont perpendiculaires.
Par conséquent, les droites $(DB)$ et $(DE)$ sont perpendiculaires. - Dans le triangle $ADE$ rectangle en $D$ on applique le théorème de Pythagore.
$AE^2=AD^2+DE^2$ soit $19,2^2=9,6^2+DE^2$
Ainsi $DE^2=19,2^2-9,6^2$ soit $DE^2=276,48$.
L’aire du triangle $ADE$ est donc :
$\begin{align*} \mathscr{A}&=\dfrac{AD\times DE}{2} \\
&=\dfrac{9,6\times \sqrt{276,48}}{2} \\
&\approx 80\end{align*}$
L’aire du triangle $ADE$ est environ égale à $80$ cm$^2$.
Exercice 4 : (points) Scratch
Dans cet exercice, toutes les longueurs sont exprimées en pixel.
Partie A :
Un professeur donne à ses élèves un motif en forme de parallélogramme et le script, en partie rédigé, qui permet de tracer ce motif. On précise que le lutin est au point de départ, comme indiqué sur la figure ci-dessous, et qu’il est orienté vers la droite :

Recopier dans le bon ordre, sur votre copie, les instructions suivantes à insérer dans le script du motif permettant de tracer le parallélogramme ci-dessus :

Partie B
Le professeur demande ensuite à ses élèves d’intégrer ce script dans un programme de leur choix permettant de tracer des figures composées de plusieurs de ces motifs.
Voici les programmes écrits par deux élèves.

On rappelle que « s’orienter à $90$ » signifie que l’on est orienté vers la droite.
- Quelle action au clavier permet de lancer le programme de l’élève B ?
- Parmi les figures suivantes, indiquer, ici sans justifier :
a. laquelle est obtenue avec le programme de l’élève A ?
b. laquelle est obtenue avec le programme de l’élève B ?
Partie A
On obtient le bloc d’instructions suivant :

$\quad$
Partie B
- Pour lancer le programme de l’élève B il faut appuyer sur la barre espace.
$\quad$ - a. On obtient la figure $1$ avec le programme de l’élève A.
$\quad$
b. On obtient la figure $4$ avec le programme de l’élève B.
$\quad$
Exercice 5 : ( 25 points) Arithmétique – Volume
Pour fêter les 25 ans de sa boutique, un chocolatier souhaite offrir aux premiers clients de la journée une boîte contenant des truffes au chocolat.
- Il a confectionné $300$ truffes : $125$ truffes parfumées au café et $175$ truffes enrobées de noix de coco.
Il souhaite fabriquer ces boîtes de sorte que :
$\bullet$ Le nombre de truffes parfumées au café soit le même dans chaque boîte ;
$\bullet$ Le nombre de truffes enrobées de noix de coco soit le même dans chaque boîte ;
$\bullet$ Toutes les truffes soient utilisées.
a. Décomposer $125$ et $175$ en produit de facteurs premiers.
b. En déduire la liste des diviseurs communs à $125$ et $175$.
c. Quel nombre maximal de boîtes pourra-t-il réaliser ?
d. Dans ce cas, combien y aura-t-il de truffes de chaque sorte dans chaque boîte ?
Le chocolatier souhaite fabriquer des boîtes contenant $12$ truffes. Pour cela, il a le choix entre deux types de boîtes qui peuvent contenir les $12$ truffes, et dont les caractéristiques sont données ci-dessous :

- $\quad$
Dans cette question, chacune des $12$ truffes est assimilée à une boule de diamètre $1,5$ cm.
À l’intérieur d’une boîte, pour que les truffes ne s’abîment pas pendant le transport, le volume occupé par les truffes doit être supérieur au volume non occupé par les truffes.
Quel(s) type(s) de boîte le chocolatier doit-il choisir pour que cette condition soit respectée ?
$\begin{array}{|l|}
\hline
\textbf{Rappels :}\\
\text{Le volume d’une boule de rayon }r \text{ est } : \dfrac{4}{3}\times \pi\times r^3 \\
\text{Le volume d’une pyramide est : }\dfrac{\text{aire de la base}\times \text{hauteur}}{3} \\
\text{Le volume d’un pavé droit est : }\text{longueur}\times \text{largeur}\times \text{hauteur} \\
\hline
\end{array}$
- a. On a
$\begin{align*} 125&=5\times 25 \\
&=5^3\end{align*}$
$\begin{align*} 175&=5\times 35\\
&=5^2\times 7\end{align*}$
b. Les diviseurs communs à $125$ et $175$ sont : $1$, $5$ et $25$.
c. Le nombre de boîtes doit diviser $125$ et $175$ et être le plus grand possible.
D’après la question précédente, le PGCD de $125$ et $175$ est $25$.
On pourra donc réaliser au maximum $25$ boîtes.
d. $\dfrac{125}{25}=5$ et $\dfrac{175}{25}=7$.
Il y aura donc $5$ truffes parfumées au café et $7$ truffes enrobées de noix de coco dans chaque boîte. - Le rayon d’une truffe est $r=\dfrac{1,5}{2}=0,75$ cm.
Le volume d’une truffe est donc :
$\begin{align*} V_T&=\dfrac{4}{3}\times \pi \times 0,75^3 \\
&\approx 1,77 \text{ cm}^3\end{align*}$
Le volume des $12$ truffes est :
$\begin{align*} V_D&=12V_T \\
&\approx 21,21\end{align*}$
Le volume de la pyramide est :
$\begin{align*} V_C&=\dfrac{1}{3}\times 4,8^2\times 5 \\
&\approx 38,4\text{ cm}^3\end{align*}$
Si on utilise cette boîte le volume non occupé par les truffes est :
$\begin{align*} V_1&=V_C-V_D\\
&\approx 17,19\\
&\pp V_D\end{align*}$
Le volume du pavé droit est :
$\begin{align*} V_P&=5\times 3,5^2 \\
&=61,25\text{ cm}^3\end{align*}$
Si on utilise cette boîte le volume non occupé par les truffes est :
$\begin{align*} V_1&=V_P-V_D\\
&\approx 40,04\\
&>V_D\end{align*}$
On ne peut donc utiliser que la boîte pyramidale.
$\quad$
